Intuition of 3x3Matrix Transformations
Rotations can be achieved by locking the desired axes of rotation and transforming the rest of the axes by \(sin\) and \(cos\).
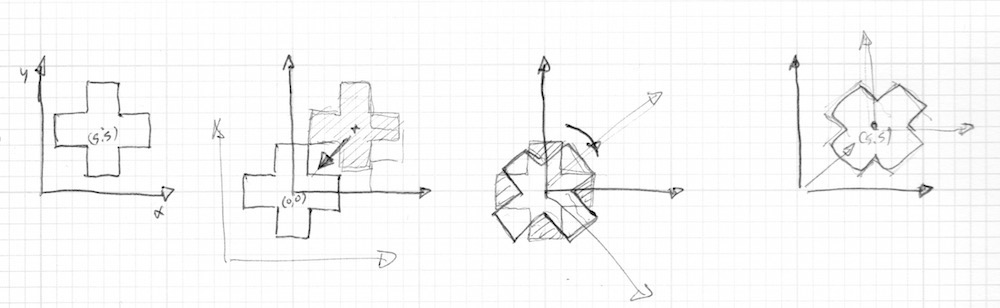
3x3 matrices can be used to bend the coordinate space in 3 dimensions, effectively allowing any desired transformations to objects in that space.
As the coordinate space is being transformed, it’s helpful breaking up the matrix into its unit vectors
$$ \vec{a} = x\begin{bmatrix}1\\0\\0\end{bmatrix} + y\begin{bmatrix}0\\1\\0\end{bmatrix} + z\begin{bmatrix}0\\0\\1\end{bmatrix} $$
Imagine taking a 1x1x1 unit cube from our coordinate space and aligning each of the sides to the given unit vectors of the matrix. Every unit in our coordinate space will be the same and any vectors within that space will have each component vector scaled.
The Rotation Matrix
The same idea applies if we want to rotate our coordinate space. We want to be able to translate each unit axis in a circle based off of some angle. Remember at each point of a unit circle, height is equal to \(sin\theta\) and width is equal to \(cos\theta\). We can can then use those as our vector inputs to follow a constant circle based off of \(\theta\).
We get the following matrices for rotating about each axis of rotation.
$$\def\rmatrices{ R_x(\theta) = \begin{bmatrix} 1 & 0 & 0\\ 0 & cos\alpha & -sin\beta\\ 0 & sin\gamma & cos\phi\\ \end{bmatrix} R_y(\theta) = \begin{bmatrix} cos\alpha & 0 & sin\beta\\ 0 & 1 & 0\\ -sin\gamma & 0 & cos\phi\\ \end{bmatrix} R_z(\theta) = \begin{bmatrix} cos\alpha & -sin\beta & 0\\ sin\beta & cos\phi & 0\\ 0 & 0 & 1\\ \end{bmatrix} } \rmatrices $$
Let’s take a look at how the \(R_z(\theta)\) matrix was formed as it’s the easiest to visualize since looks like a 2D rotation. If we want to rotate by an axis, we don’t want any coordinate on that axis to move while everything rotates around it.
Therefore we set the zcomponent to \(\begin{bmatrix}0\\0\\1\end{bmatrix}\) to multiply any values on it by 1.
Sandbox Example
threejs$$\rmatrices$$