I’ve always had trouble understanding probability, especially when entering into the more theoretical aspects of it. Here, I want to cover some of the basic concepts and functions core to probability in an easily digestible format that I can refer to later on when I inevitably forget it all.
Random Variable
Whenever there’s a question of probability, you tend to have some range of possible outcomes sourced from a specific event.
We label some process that has multiple outcomes as a random variable.
Typically, we use \(X\) to name this random variable though it can be any name capitalized as convention.
An easy example is a six-sided die where there are precisely six possible outcomes. In essence, our random variable can be thought of as a list of these outcomes.
X = [1, 2, 3, 4, 5, 6]
Expected Value
As the name suggests, this averages out the probabilities of all the outcomes and returns the mean (\(\mu\)) of all the outcomes.
$$E[X] = \sum_{x} P(X=x)*x$$
For example, in the case of a six-sided fair die, the probability of each outcome is uniform leading to the following expected value.
$$E[X] = \frac{1}{6}(1 + 2 + 3 + 4 + 5 + 6) = 3.5$$
The average roll is 3.5
Variance
To preface, standard deviations and variance are nearly identical and both describe the dispersion of values. Standard deviation is often more useful in applications and visualizations than variance. However, standard deviations is derived from variance so it’s important to know what variance is though, seeing the purpose of variance this way can be difficult. Rather, comprehend the math of variance in relation to expected value, and then move on to standard deviation to understand its usefulness.
The variance tells us how spread out a probability distribution is. We do this by finding the difference between each outcome and the expected value (\(\mu\)), and then take that expected value (in other words, we get the average difference each outcome is from the mean).
$$V(X) = E[(X - \mu)^2] = \sum_{x} P(X=x)*(x-\mu)^2$$
You may notice that we actually square that difference. Other than ensuring our difference is positive, taking square makes the math nicer later on.
In the case of a fair die, we get the following variance.
$$V(X) = \frac{1}{6}(17.5) = \frac{35}{12}$$
the squared distance between each die face and the mean is 2.916.
Standard Deviation
Let’s start with this comparison with variance.
$$\sigma = \sqrt{V(X)}$$
When we talk about variance being the average difference from the mean, it can be difficult to picture as it is the squared distance from the mean. Instead, if we want to normalize the units we take the standard deviation as the square root of the variance.
Now when we say the average distance each result is from the mean, we can properly denote it as \(n\) standard deviations away from the mean.
From the prior die example, we get this standard deviation
$$\sigma = \sqrt{\frac{35}{12}} = 1.71$$
Now let’s say we roll a 1 which deviates from the mean by 2.5, comparing this to our standard deviation we get the following
$$\frac{2.5}{\sigma} = 1.46$$
Our dice roll of 1 was roughly 1.46 standard deviations away from the mean which is actually just another way to say it was 2.5 away from the mean like we started.
Statistical Uses
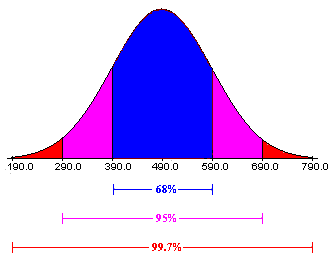
Those who work with probabilities on large datasets are generally familiar with how data fits within a range of standard deviation. The chart above is saying:
- 68% of values are within 1 \(\sigma\) away from the mean
- 95% of values are within 2 \(\sigma\) away from the mean
- 99.7% of values are within 3 \(\sigma\) away from the mean
Knowing the standard deviation gives great insight into how clustered dataset is around the mean. Larger values suggest a more spread out dataset.
Conditional Probabilities
Conditional probabilities ask, “what is the probability of A given a condition B”.
More formally,
$$P(A|B) = \frac{P(A\cap B)}{P(B)}$$
The intuition is that we’re looking at subset of the data that satisfies this condition B. Then, we’re taking a fraction of those that satisfy A within the subset B.
Bayes Theorem
$$P(A|B) = \frac{P(B|A)P(A)}{P(B)}$$
The thing you might notice is that we’re also describing conditional probabilities, so what’s the difference?
Instead of using the joint probability \(P(A\cap B)\), we use the reverse condition \(P(B|A)P(A)\). But these are actually equivalent! Think about it this way: The probability of A and B happening is the same thing as saying the probability of A happening and the probabilty of B given that A happened.
But what’s the point?
Bayes Theorem is better suited to conditional problems where our condition updates our original probability. In other words, we can visualize the probability as a hypothesis and a piece of evidence. We can repeatedly update our probability as new evidence comes in.
$$P(A\cap B) = P(B|A)P(A) = P(New\ evidence\ after\ current\ event)P(current\ event)$$
An Example
Let’s say our hypothesis is that Anne is a vegetarian and let’s say that 1/4 of people are vegetarians. Then the probability of Anne being one is just so.
$$P(H) = 1/4$$
Now, let’s say we get some evidence that Anne is a climate change activist. Now the question is, “what’s the probability that Anne is a vegetarian given that she’s also a climate change activist (activist for short).
Let’s say we infer that a fifth of vegetarians are activists and a tenth of non-vegetarians are activists. Then we can solve as follows
$$P(H|E) = \frac{P(Vegetarian)P(Activist\ if\ Vegetarian)}{P(Activist)} = \frac{\frac{1}{4}*\frac{1}{5}}{\frac{1}{5}+\frac{1}{10}} = \frac{1}{6}$$
Imagine from here, we can repeat the process with new evidence using the previous evidence as our hypothesis instead, further refining our probability. This forms the basis of many uses cases like risk analysis and machine learning.'
